|
|
 |

|
 |
 |
| Perceptual Optimization of Wavelet Image Compression (Andrew B. Watson, Gloria Y. Yang, Joshua A. Solomon, & John Villasenor) |
 |
NASA's extensive image compression requirements may be met in part by the use of wavelet techniques.(1) Wavelets form a large class of signal and image transforms, generally characterized by decomposition into a set of self-similar signals that vary in scale and (in 2D) orientation. (2) The Discrete Wavelet Transform (DWT) is a particular member of this family which operates on discrete sequences, and which has proven to be an effective tool in image compression. (3, 4)
Under a grant from NASA's Life and Biomedical Sciences and Applications Division, and in collaboration with university partners, we have undertaken a program of research to optimize wavelet compression for the human viewer.
The Discrete Wavelet Transform (DWT) decomposes an image into bands that vary in spatial frequency and orientation. In a typical compression application, an image is subjected to a two-dimensional DWT whose coefficients are then quantized and entropy coded. Measures of the visibility of DWT quantization errors are required to achieve optimal compression. Uniform quantization of a single band of coefficients results in an artifact that is the sum of a lattice of random amplitude basis functions of the corresponding DWT synthesis filter, which we call DWT uniform quantization noise. We measured visual detection thresholds for samples of DWT uniform quantization noise in Y, Cb, and Cr color channels.
The spatial frequency of a wavelet is r 2-L , where r is display visual resolution in pixels/degree, and L is the wavelet level. Amplitude thresholds increase rapidly with spatial frequency. Thresholds also increase from Y to Cr to Cb, and with orientation from low-pass to horizontal/vertical to diagonal.
We propose a mathematical model for DWT noise detection thresholds that is a function of level, orientation, and display visual resolution. This allows calculation of a "perceptually lossless" quantization matrix for which all errors are in theory below the visual threshold. The model may also be used as the basis for adaptive quantization schemes. A more detailed description of this work is available.
Figure 1 shows perceptually lossless wavelet quantization factors computed from the model for three visual resolutions. Different symbols indicate different wavelet orientations. At low visual resolution, factors are nearly constant with level and orientation. At high resolutions, factors vary markedly with both level and orientation.
Figure 2. shows an example color image compressed with perceptually lossless DWT quantization matrix (left) and twice that matrix (right). At the appropriate viewing distance (about seven picture heights) the picture on the left should appear lossless, while the one on the right should have visible artifacts.
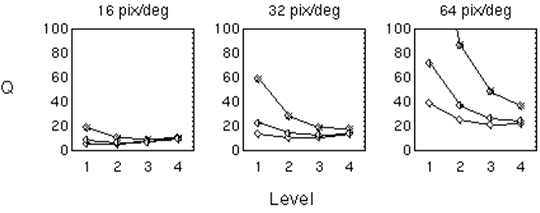
Figure 1. Perceptually lossless wavelet quantization factors at three visual resolutions. Different symbols indicate different wavelet orientations.

Figure 2. Image compressed with perceptually lossless DWT quantization matrix (left) and twice that matrix (right). Image dimensions are 256x256 pixels. Quantization matrix is designed for a viewing distance of about seven picture heights.
References
- A. Jaworski, "Earth Observing System (EOS) Data and Information System (DIS) software interface standards," AIAA/NASA Second International Symposium on Space Information Systems, Proceedings, AIAA-90-5075, (1990).
- S.G. Mallat,"Multifrequency channel decompositions of images and wavelet models," IEEE Transactions on Acoustics, Speech, and Signal Processing, 37(12), 2091-2110 (1989).
- T. Hopper, C. Brislawn and J. Bradley, "WSQ grey-scale fingerprint image compression specification, Version 2.0," Criminal Justice Information Services, Federal Bureau of Investigation, Washington, DC. (1993).
- M. Antonini, M. Barlaud, P. Mathieu and I. Daubechies,"Image coding using the wavelet transform," IEEE Transactions on Image Processing, 1, 205-220 (1992).
- A.B. Watson, G.Y. Yang, J.A. Solomon and J. Villasenor,"Visual Thresholds for Wavelet Quantization Error," Human Vision and Electronic Imaging, B. Rogowitz and J. Allebach, 2657, paper # 44, The Society for Imaging Science and Technology, (1996).
|
|
|
|
|