|
|
 |
|
|
 |
 |
(May 21, 2010)
Andrew B. Watson, Ph.D. - Senior Scientist for Vision Research |
| |
 |
Workers in public safety- police, firefighters, homeland security personnel, NASA safety officials - often make use of video systems to monitor the environment or to document their activities. Whatever the purpose, the quality of the captured imagery is of paramount importance. In this note, we provide a brief, non-technical human factors perspective on some of the issues that determine video quality in public safety applications.
We begin with an image in Figure 1, as it might be captured by a video system. In this picture, we see a person, and if we look closely, we see in their hand, what might be a gun. |

Figure 1. An example image, containing the field of view. |
Task
In most applications there is a task. In this case the task might be to determine whether there is there a gun in the person's hand. For purposes of this note, the question we would like to answer is: what video conditions will allow us to perform this task?
Field of view
The first question we must ask is: how big is the space being viewed? In general, in a surveillance application, there is region of the world that we want to observe. We call this the "field of view." Let's assume that the picture above encloses the field of view. To measure the field of view in this example, we might say it is 25 feet wide at a distance of 30 feet.
In the camera world, the field of view usually gets translated into an "angular" field of view. This is the angle that encloses that width at that distance. It is easy to get the angle from this approximation:
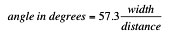
so in this example it is angle = 57.3 25/30 = 47.75 degrees.
Target
There is something in this image that we are interested in; we will call this the target. In this case, it is the gun. Clearly it is much smaller that the field of view. In Figure 2 we have extracted the target in an area 1/24 as wide as the field of view. The actual target occupies only about half that width, so it is about 1/48 as wide as the field of view.
|

Figure 2. The target, extracted from the larger image, and magnified by 2, 4, and 8. |
Critical Resolution
Now lets suppose that we can analyze the image offline. We can enlarge the image of the target so that it is as big as we want. (Figure 2). Eventually, the picture becomes blocky. All modern digital video systems capture the image as an array of pixels. Each pixel is a (usually) square dot of uniform color. Usually, the pixels are very small, and blend together to form a smooth image. But when the image is enlarged, we can see the pixels.
Since enlarging the individual pixels doesn't provide more information, or make patterns more visible, we must complete the task with the finite number of available pixels covering the target. The question is then: how many pixels do we need to do the task? It turns out that for each task there is a critical number: we will call this the critical resolution, measured in pixels/target width. The more difficult or demanding the task, the larger then number of pixels required. For this reason, we can use critical resolution as the measure of the task difficulty, also called "discrimination level."
Lets take a moment to appreciate that different tasks can have very different critical resolutions. To tell whether it is day or night in the scene, we are likely to need only a single pixel. Distinguishing a gun from a cell phone might require 10 pixels. To recognize the face of a particular person, from among three possible faces, might only require four pixels. But to identify a particular person, from among a hundred million, might require a critical resolution of hundreds of pixels. To ensure that your video system enables your task, you must ensure that it provides the critical resolution for your task. What determines the critical resolution of a video system? We have already seen the role of the target size and the field of view. If we call the critical resolution R (in pixels), and the size of the target S (in fractions of the field of view), then the camera must capture an image at least R/S pixels wide. In our example, the gun is S = 1/48 of the field of view, and we assume the critical resolution is R = 10 pixels, then we need a camera resolution of at least 10 x 48 = 480 pixels. In the example above, we began with a camera resolution of 960, so we should be ok.
Camera Properties
But what determined the field of view of the camera? A digital camera consists of a lens, an aperture, a shutter, and a sensor. The lens focuses the light from the world, through the aperture, and onto the electronic sensor that converts the image into an array of pixels. The angular field of view is established by fundamental camera properties of focal length and sensor size. Typical camera lenses are either "wide angle" to capture a wide angle of view, or "telephoto", to capture a narrow angle of view, or something in between, called "normal", which is about 50 degrees. The focal length and sensor size also determine the optical magnification, since either a wide or narrow angle is being imaged on the same size sensor. In a zoom lens, the field of view can be varied as needed within some range. So a camera lens and sensor must be selected that will yield the desired field of view.
Optical Blur
To this point we have spoken as though camera pixels were perfect measurements of light at a point in the field of view. Unfortunately, that is never true. Any real lens blurs the image by a certain amount. Figure 3 shows our target in the presence of two amounts of optical blur. This blur depends on how well the lens is focussed, but also on the resolution of the sensor, and imperfections of the lens (called aberrations) that tend to increase as the lens gets smaller, lighter, and cheaper.
|

Figure 3. Target image with increasing amounts of blur.
|
What does blur have to do with critical resolution? Critical resolution really depends on the number of "effective pixels" across the target. In effect, blur smears the image across several pixels, and thus reduces the number of effective pixels. For example, if the blur smeared the image across two pixels, then there would be only half as many effective pixels across the captured image, and to achieve our desired critical resolution we would now need a captured image with 960 pixel width.
Visual Blur
What if the image cannot be scrutinized offline, and zoomed up to a desired size? In many applications the video is viewed live, with little opportunity for processing or enhancement. In such situations, the need for critical resolution remains, but it must take into account the limitations of the human eye as well. To a first approximation, this can be thought of as an additional source of blur. The amount of blur depends on the size of the pixels, and the distance from the eye to the display. In these situations, the ability to do the task depends on the display, as well as the camera and network.
Noise
Another camera property that affects critical resolution is noise. Noise is an unavoidable variability in the value of each pixel. If you took the same picture twice, individual pixel values would be different. Noise makes it more difficult to identify targets. As with blur, we can think of noise as reducing the number of effective pixels in the image. To make the discrimination, we have to increase the camera resolution. In Figure 4, we show the gun target with small and large amounts of noise.
|

Figure 4. Target with small and large amounts of noise.
|
The noise in each camera pixel is determined by the size of the aperture (bigger = less noise), the size of the sensor (bigger = less noise), the type of sensor (ccd less than cmos), the number of pixels in the sensor (fewer = less noise), the light level in the field of view (brighter = less noise), and the shutter speed (longer = less noise). Just as with blur, we can think of the noise as reducing the number of effective pixels, thus mandating a higher initial capture resolution.
Motion Blur
Another source of blur is motion. If the target moves while light is being measured by the sensor, then the image can be smeared over several pixels. Just as with optical blur, this reduces the effective resolution of the captured image. Simple calculations give an idea of this effect. Suppose the captured image is 1000 pixels wide. If the field of view is 25 feet, and the target moves at 9 inches in one second, and the shutter is open for 1/30 of a second, that works out to a movement of (1/30)(9/12)(1000/25) = 1 pixel in one frame time. So each pixel will be blurred into two pixels, and the number of effective pixels will be cut in half.
Compression
In a digital video system, the data are almost always compressed, to reduce the file size and bandwidth requirements. Familiar compression formats are JPEG (for still images) and MPEG-2, H.262, and H.264. Compression consists of algorithms to reduce the number of bits required to represent a video clip, either by removing redundancy or parts that the eye cannot see. Figure 5 shows an example of severe compression of our example target image. The compression artifacts make the target harder to identify.
|

Figure 5. The more compressed target image on the right is harder to identify.
|
Usually the compression settings of a video system are set to provide a reasonably high quality experience when the video is viewed live at a normal distance. The apparent quality may be much poorer if individual frames are extracted and magnified. This must be taken into account when selecting compression parameters or predicting ultimate task performance.
Critical Frame Rate
Conventional video is captured at a frame rate of 30 frames/second. To capture very rapid motion or change, specialized cameras with much higher frame rates are available, though they usually entail a cost in terms of dollars, spatial resolution, or both. Likewise, if the targets in the field of view change very slowly, a slower frame rate can be considered. This is often done to reduce the storage or bandwidth requirements. As with spatial resolution, we can think in terms of a critical temporal resolution (critical frame rate) required to do the task.
Summary
In this discussion we have made many simplifications, and we have not explained in detail how to determine critical resolution for a task or a video system. But the purpose has been to give an intuitive introduction to how the size of the target, the field of view, and fundamental video system properties combine to determine the ability to do the task. Sometimes it is possible to calculate or simulate the performance of a camera system in the relevant application, though it is usually necessary to confirm these calculations in the field.
|
References and further reading
Huck, F. O., Fales, C. L., Halyo, N., Samms, R. W., & Stacy, K. (1985). Image gathering and processing: information and fidelity. J Opt Soc Am A, 2(10), 1644-1666.
Johnson, J. (1958). Analysis of image forming systems Image Intensifier Symposium, AD 220160(pp. 244-273): Warfare Electrical Engineering Department, U.S. Army Research and Development Laboratories, Ft. Belvoir, Va.
Schade, O. (1958). On the quality of color-television images and the perception of colour detail. Journal of the Society of Motion Pictures and Television Engineers, 67(12), 801-819.
Watson, A. B., & Ahumada, A. J., Jr. (2008). Predicting visual acuity from wavefront aberrations. Journal of Vision, 8(4), 1-19.
Useful Link
http://www.pscr.gov/projects/video_quality/video_about.php |
|
|
|